Mighty is geometry — joined with art, irresistible.
— Euripides (480-406 BCE)
The idea of ‘Sacred Geometry’ is that mathematics can be beautiful. For example, here’s one of the most famously beautiful equations in mathematics:
eiπ + 1 = 0
It’s called “Euler’s Identity,” after the Swiss mathematician Leonhard Euler (1707-1783, pronounced “OIL-er”) who first discovered it. You have to be far into math for this equation just to make sense, much less to find it beautiful.
Geometry is another story. Here’s a geometrically generated image:
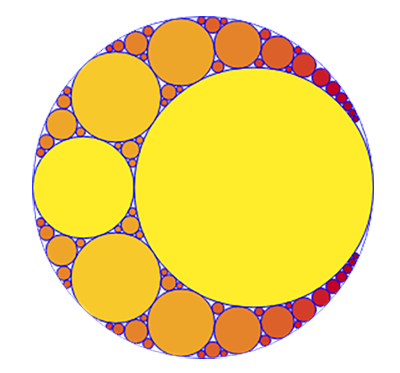
This is called the “Apollonian Gasket,” named after Apollonius of Perga (c.240 – c.190 BCE), an ancient Greek geometer and astronomer who laid the mathematical groundwork for it. (Perga is in present day Türkiye). No math background is necessary to grasp its beauty.
So mathematicians might argue that all of mathematics is beautiful. But from a pragmatic point of view, geometric images are accessible to non-mathematicians. No math background necessary to enjoy them!
Plato
One of Plato’s most famous ideas is that there are “Forms” (aεἶδος” (eidos) or ἰδέα” (idea)) — abstract, perfect, and unchanging concepts or ideals exist in a separate, non-physical realm, serving as the true essence and blueprint for all imperfect and transient objects and qualities down here in the interior material world. Plato believed that mathematics, with its focus on abstract, eternal, and unchanging truths, serves as a crucial bridge to understanding this higher realm of Forms, exemplifying the nature of these ideal entities. Not everyone agrees with this, but the idea has been very persistent in Western philosophy ever since.
Pythagoras
Pythagoras, the Greek mathematician and philosopher, is often credited with advancing the study of sacred geometry. His famous theorem about right-angled triangles reflects a deeper belief in the harmony and order of numbers. Pythagoras and his followers saw numbers and geometric forms as keys to understanding the divine order of the universe, coining the term “mathematikos,” meaning “that which is learned.”
((We’re not sure exactly what was discovered by Pythagoras himself, or by his students at his ‘Pythagorean School’ which lasted several centuries.)
We all learned Pythagoras’ famous theorem about right triangles in high school: a2 + b2 = c2. The Egyptians and Babylonians had observed this for over a millenium before Pythagoras. What makes Pythagoras’ theorem significant is their invention of the ‘mathematical proof.” Before Pythagoras many had observed that a2 + b2 = c2 was true in every instance they had checked, but the possibility always remained that in the next right triangle this would not be so. The Pythagoreans proved that it must ALWAYS be so.
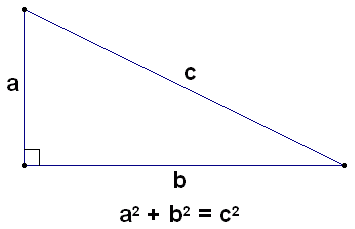
Although the ancient Babylonians and Egyptians knew about the theorem practically, the Pythagoreans are credited with providing a formal proof of the theorem, transforming it from an empirical observation into a rigorously demonstrated mathematical truth. This approach marked a significant advancement in the development of mathematics as a deductive science.
(The Pythagoreans were also very interested in the mystical properties of numbers.)
So it shouldn’t be surprising that architects would use geometric patterns and ratios in the design of temples, mosques and cathedrals — as ways of trying to portray the Infinite. Around the 1970’s the term “sacred geometry” was coined for this overlap of geometry, art and spirituality, and the name has stuck.
Sacred Geometry in Nature
Sacred geometers would argue that it is not merely a theoretical construct; it is observed throughout the natural world. The spiral patterns of shells, the branching of trees, the symmetry of flowers, and the crystalline structures of minerals all reflect geometric principles. These patterns are seen as evidence of an underlying order and intelligence in the cosmos.
For example, the Fibonacci sequence, a series of numbers where each number is the sum of the two preceding ones, is closely related to the golden ratio. This sequence appears in the arrangement of leaves on a stem, the flowering of artichokes, the arrangement of a pine cone’s scales, and the pattern of a sunflower’s seeds.
Consequently, sacred geometry is often used as a tool for meditation and contemplation. The contemplation of geometric patterns is believed to bring individuals into harmony with the natural world and the cosmos, fostering a sense of peace, balance, and unity. Many cultures have used geometric mandalas and yantras as meditative aids, believing that these shapes can help align the mind and soul with higher spiritual realities.
Modern Relevance and Applications
Today, sacred geometry continues to inspire artists, architects, and spiritual seekers. It is seen in the designs of modern architecture, art installations, and digital media. The principles of sacred geometry are also being explored in the fields of quantum physics, cosmology, and chaos theory, suggesting a deep connection between ancient wisdom and modern science.
In the realm of personal spirituality, sacred geometry offers metaphors for exploring the interconnectedness of all life and the universe. It encourages individuals to see the beauty and order in the world around them and to recognize their place within a larger cosmic pattern.



Leave a Reply